🎛️ Rumus Slovin (Untuk Survei)
🔍 Penjelasan Lengkap
Kapan Digunakan: Rumus Slovin digunakan untuk menghitung ukuran sampel yang diperlukan dalam penelitian survei, ketika jumlah total populasi sangat besar dan tidak mungkin untuk menyurvei seluruh populasi. Dengan rumus ini, peneliti dapat menentukan jumlah sampel yang cukup representatif dengan mempertimbangkan margin kesalahan yang diinginkan.
Contoh Penerapan (Studi Kasus): Misalkan sebuah kota memiliki populasi sebesar 50.000 orang, dan peneliti ingin mengukur preferensi pemilih terhadap kandidat dalam pemilihan umum dengan margin kesalahan 5% (e = 0.05). Dengan menggunakan Rumus Slovin, peneliti dapat menghitung ukuran sampel yang diperlukan untuk penelitian tersebut.
Kelebihan dan Kelemahan:
✅ Kelebihan:
• Sangat mudah digunakan untuk penelitian survei dengan populasi besar.
• Tidak memerlukan informasi tentang varians populasi.
❌ Kelemahan:
• Tidak selalu akurat jika populasi tidak homogen atau data tidak terdistribusi secara acak.
• Margin kesalahan yang lebih kecil membutuhkan sampel yang lebih besar.
Referensi:
• Tejada, J. J., & Punzalan, J. R. B. (2012). On the misuse of Slovin’s formula.The philippine statistician, 61 (1), 129-136.
• Ryan, T. P. (2013).Sample size determination and power. ohn Wiley & Sons.
Formula:
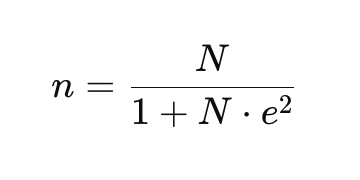 Di mana:
Di mana:
- n = jumlah sampel.
- N = ukuran populasi.
- e = margin kesalahan yang diinginkan (misalnya, 0.05 untuk 5%).
🎛️ Perhitungan Sampel untuk Proporsi Tunggal (Single Proportion)
🔍 Penjelasan Lengkap
Kapan Digunakan: Digunakan untuk menghitung ukuran sampel yang diperlukan ketika penelitian ingin memperkirakan proporsi suatu kejadian dalam populasi. Misalnya, peneliti ingin mengetahui proporsi orang yang memilih suatu kandidat politik, atau proporsi keberhasilan dalam percobaan.
Contoh Penerapan (Studi Kasus): Sebuah survei ingin mengukur proporsi pemilih yang mendukung kandidat politik tertentu. Dari survei awal, diperkirakan 60% pemilih akan mendukung kandidat tersebut. Peneliti ingin menggunakan tingkat kepercayaan 95% dan margin of error 5%. Maka perhitungan ukuran sampel dapat dilakukan dengan rumus ini.
Kelebihan dan Kelemahan:
✅ Kelebihan:
• Sederhana dan mudah digunakan untuk estimasi proporsi.
• Cocok untuk penelitian sosial dan pemilu.
❌ Kelemahan:
• Membutuhkan estimasi proporsi awal yang mungkin tidak selalu akurat.
• Tidak berlaku untuk perbandingan antara dua kelompok atau lebih.
Referensi:
• Gonçalves, L., de Oliveira, M. R., Pascoal, C., & Pires, A. (2012). Sample size for estimating a binomial proportion: comparison of different methods. Journal of Applied Statistics, 39 (11), 2453-2473.
• Vasudevan, S. (2024). Sample size calculation in various medical research. International Journal of Medical Sciences and Nursing Research, 4 (3), 22-29.
Formula:
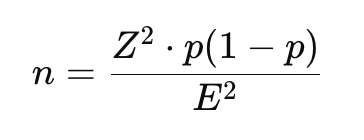 Di mana:
Di mana:
- n = jumlah sampel yang dibutuhkan.
- Z = skor Z untuk tingkat kepercayaan (misalnya, 1.96 untuk 95% confidence level).
- p = perkiraan proporsi dalam populasi.
- E = margin kesalahan yang diinginkan (misalnya, 0.05 untuk 5%).
🎛️ Perhitungan Sampel untuk Dua Proporsi (Two Proportions)
🔍 Penjelasan Lengkap
Kapan Digunakan: Digunakan ketika peneliti ingin membandingkan dua proporsi (persentase) antara dua kelompok yang independen. Contohnya, membandingkan tingkat keberhasilan suatu pengobatan (proporsi sembuh) antara dua kelompok yang diberi pengobatan berbeda.
Contoh Penerapan (Studi Kasus): Sebuah penelitian ingin mengetahui apakah ada perbedaan proporsi keberhasilan antara dua jenis vaksin dalam mencegah infeksi. Diketahui bahwa proporsi keberhasilan vaksin A adalah 80% (P1), sedangkan vaksin B memiliki proporsi keberhasilan 70% (P2). Peneliti menggunakan tingkat signifikansi 5% dan kekuatan uji 80%.
Kelebihan dan Kelemahan:
✅ Kelebihan:
• Dapat digunakan untuk perbandingan antara dua proporsi dalam populasi yang berbeda.
• Cocok untuk studi klinis atau eksperimen yang melibatkan kategori binomial (misalnya, sukses/gagal).
❌ Kelemahan:
• Asumsi independensi antara dua kelompok harus dipenuhi.
• Membutuhkan estimasi proporsi yang cukup akurat untuk menghitung ukuran sampel dengan benar.
Referensi:
• Gonçalves, L., de Oliveira, M. R., Pascoal, C., & Pires, A. (2012). Sample size for estimating a binomial proportion: comparison of different methods. Journal of Applied Statistics, 39 (11), 2453-2473.
• Vasudevan, S. (2024). Sample size calculation in various medical research. International Journal of Medical Sciences and Nursing Research, 4 (3), 22-29.
Formula:
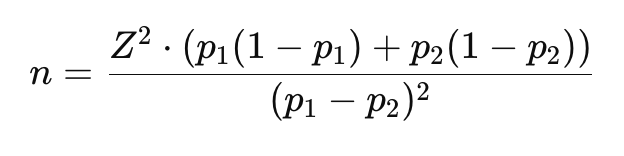 Di mana:
Di mana:
- p1 dan p2 = proporsi dalam dua kelompok yang dibandingkan.
- n = jumlah sampel per kelompok.
- Z = skor Z untuk tingkat kepercayaan (misalnya, 1.96 untuk 95% confidence level).
🎛️ Perhitungan Sampel untuk Dua Rata-Rata Independen
🔍 Penjelasan Lengkap
Kapan Digunakan: Digunakan ketika peneliti ingin membandingkan dua rata-rata dari dua kelompok yang independen (tidak saling berhubungan), misalnya kelompok kontrol vs. kelompok perlakuan. Metode ini berguna dalam uji hipotesis parametrik untuk membuktikan adanya perbedaan yang signifikan secara statistik antara kedua kelompok.
Contoh Penerapan (Studi Kasus): Sebuah penelitian ingin mengetahui perbedaan rata-rata kadar gula darah antara pasien yang diberikan obat A dan pasien yang diberikan obat B. Diketahui varians populasi dari kedua kelompok, tingkat signifikansi 5% (Zα/2 = 1.96), serta kekuatan uji 80% (Zβ = 0.84). Perbedaan rata-rata yang dianggap signifikan adalah 10 mg/dL.
Kelebihan dan Kelemahan:
✅ Kelebihan:
• Memungkinkan perbandingan dua kelompok secara langsung dengan mempertimbangkan variasi data.
• Cocok untuk desain penelitian eksperimental sederhana.
❌ Kelemahan:
• Membutuhkan asumsi normalitas distribusi dan homogenitas varians kedua kelompok.
• Perlu data varians populasi yang sering kali tidak selalu tersedia.
Referensi:
• Gonçalves, L., de Oliveira, M. R., Pascoal, C., & Pires, A. (2012). Sample size for estimating a binomial proportion: comparison of different methods. Journal of Applied Statistics, 39 (11), 2453-2473.
• Vasudevan, S. (2024). Sample size calculation in various medical research. International Journal of Medical Sciences and Nursing Research, 4 (3), 22-29.
Formula:
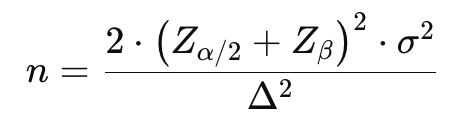 Di mana:
Di mana:
- σ2 = varians populasi.
- Δ = perbedaan rata-rata yang diinginkan antara dua kelompok.
- Zα/2 = skor Z sesuai tingkat signifikansi (misalnya 1.96 untuk 95%).
- Zβ = skor Z sesuai kekuatan uji yang diinginkan (misalnya 0.84 untuk 80%).
🎛️ Perhitungan Sampel untuk Studi Kohort
🔍 Penjelasan Lengkap
Kapan Digunakan: Perhitungan ini digunakan dalam studi kohort untuk menentukan ukuran sampel yang diperlukan agar dapat mendeteksi perbedaan signifikan antara dua kelompok berdasarkan proporsi kejadian suatu peristiwa, seperti perbandingan antara kelompok yang terpapar dan yang tidak terpapar suatu faktor risiko.
Contoh Penerapan (Studi Kasus): Sebuah penelitian ingin mengetahui apakah merokok meningkatkan risiko terkena kanker paru-paru. Kelompok pertama (eksposur) terdiri dari perokok, dan kelompok kedua (non-eksposur) terdiri dari non-perokok. Diketahui bahwa proporsi kejadian kanker paru-paru pada perokok adalah 10% (P1), sedangkan pada non-perokok adalah 2% (P2). Penelitian ini menginginkan tingkat signifikansi 5% dan kekuatan uji 80%.
Kelebihan dan Kelemahan:
✅ Kelebihan:
• Dapat digunakan untuk membandingkan kejadian penyakit atau kondisi tertentu pada dua kelompok dengan faktor eksposur yang berbeda.
• Bermanfaat untuk menentukan besar sampel yang tepat berdasarkan perbedaan proporsi kejadian.
❌ Kelemahan:
• Membutuhkan data proporsi kejadian yang akurat untuk kedua kelompok.
• Hasil dapat dipengaruhi oleh bias seleksi atau informasi jika pengumpulan data tidak hati-hati.
Referensi:
• Liu, H., Shen, Y., Ning, J., & Qin, J. (2017). Sample size calculations for prevalent cohort designs. Statistical methods in medical research, 26 (1), 280-291.
• Mitra, A. K. (2023). Sample Size Estimation. In Statistical Approaches for Epidemiology: From Concept to Application (pp. 275-292). Cham: Springer International Publishing.
Formula:
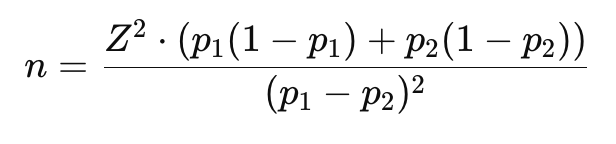 Di mana:
Di mana:
- p1 dan p2 = proporsi dari dua kelompok yang dibandingkan.
- (p1 - p2) = perbedaan proporsi yang diharapkan.
- Z = skor Z untuk tingkat kepercayaan (misalnya, 1.96 untuk 95% confidence level).
🎛️ Perhitungan Sampel untuk Studi Kasus-Kontrol
🔍 Penjelasan Lengkap
Kapan Digunakan: Digunakan untuk menghitung jumlah sampel yang dibutuhkan dalam penelitian dengan desain studi kasus-kontrol. Studi ini umumnya digunakan untuk membandingkan proporsi kejadian atau eksposur antara dua kelompok: kelompok kasus (yang memiliki penyakit atau kondisi) dan kelompok kontrol (yang tidak memiliki penyakit atau kondisi).
Contoh Penerapan (Studi Kasus): Dalam sebuah penelitian untuk mengetahui hubungan antara merokok dan kanker paru-paru, 100 orang dengan kanker paru-paru (kelompok kasus) dibandingkan dengan 100 orang yang sehat tanpa kanker paru-paru (kelompok kontrol). Peneliti ingin mengetahui proporsi orang yang merokok pada kedua kelompok tersebut. Dalam hal ini, rumus perhitungan sampel digunakan untuk menentukan ukuran sampel yang cukup agar hasilnya dapat dipercaya.
Kelebihan dan Kelemahan:
✅ Kelebihan:
• Memungkinkan perbandingan proporsi kejadian antara kelompok kasus dan kontrol.
• Sangat berguna dalam penelitian retrospektif.
❌ Kelemahan:
• Membutuhkan data yang akurat mengenai proporsi kejadian pada masing-masing kelompok.
• Bisa memerlukan banyak sampel jika perbedaan antara proporsi sangat kecil.
Referensi:
• Kubota, K., & Wakana, A. (2011). Sample-size formula for case-cohort studies. Epidemiology, 22 (2), 279.
• Woolson, R. F., Bean, J. A., & Rojas, P. B. (1986). Sample size for case-control studies using Cochran's statistic. Biometrics, 927-932.
Formula:
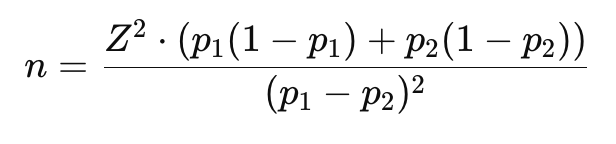 Di mana:
Di mana:
- (Formula ini mirip dengan perhitungan untuk studi kohort, digunakan untuk kasus-kontrol dengan perbedaan proporsi).
🎛️ Perhitungan Sampel untuk Studi Longitudinal
🔍 Penjelasan Lengkap
Kapan Digunakan: Perhitungan sampel untuk studi longitudinal digunakan ketika peneliti ingin mengukur perubahan dalam kelompok yang sama selama beberapa periode waktu. Studi ini berfokus pada pengukuran berulang pada individu yang sama untuk melihat efek dari intervensi atau perubahan seiring waktu.
Contoh Penerapan (Studi Kasus): Penelitian ingin mengetahui perubahan tekanan darah di kelompok pasien yang menerima pengobatan hipertensi selama 6 bulan. Data tekanan darah diukur pada tiga waktu yang berbeda. Peneliti ingin mendeteksi perubahan rata-rata tekanan darah di antara waktu tersebut dan menggunakan tingkat signifikansi 5% dan kekuatan uji 80%.
Kelebihan dan Kelemahan:
✅ Kelebihan:
• Mampu mengidentifikasi perubahan yang terjadi dalam waktu.
• Menggunakan data pengukuran berulang yang dapat meningkatkan efisiensi sampel.
❌ Kelemahan:
• Membutuhkan kontrol yang ketat terhadap faktor pengganggu yang dapat mempengaruhi pengukuran berulang.
• Memerlukan metode analisis statistik yang lebih kompleks, seperti analisis varians berulang (ANOVA) atau model campuran.
Referensi:
• Fitzmaurice, G. M., Laird, N. M., & Ware, J. H. (2011). Applied Longitudinal Analysis (2nd ed.). Wiley.
• Diggle, P. J., Heagerty, P., Liang, K. Y., & Zeger, S. L. (2002). Analysis of Longitudinal Data (2nd ed.). Oxford University Press.
Formula:
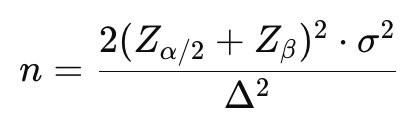 Di mana:
Di mana:
- σ2 = varians pengukuran dalam studi longitudinal.
- Δ = perbedaan yang diinginkan antara dua titik waktu.
- Zα/2 = skor Z sesuai tingkat signifikansi (misalnya 1.96 untuk 95%).
- Zβ = skor Z sesuai kekuatan uji yang diinginkan (misalnya 0.84 untuk 80%).
🎛️ Perhitungan Sampel untuk Uji T (Independent Two-Sample T-Test)
🔍 Penjelasan Lengkap
Kapan Digunakan: Uji T Independen digunakan untuk membandingkan dua kelompok yang independen (tidak saling berhubungan) berdasarkan rata-rata mereka, untuk melihat apakah terdapat perbedaan yang signifikan secara statistik. Biasanya digunakan ketika kedua kelompok tidak saling mempengaruhi satu sama lain dan memiliki distribusi data yang relatif normal.
Contoh Penerapan (Studi Kasus): Sebuah penelitian ingin mengetahui apakah terdapat perbedaan signifikan dalam rata-rata berat badan antara pria dan wanita yang mengikuti program diet yang sama. Diketahui varians berat badan dari masing-masing kelompok, tingkat signifikansi 5% (Zα/2 = 1.96), dan ukuran sampel yang akan digunakan untuk setiap kelompok.
Kelebihan dan Kelemahan:
✅ Kelebihan:
• Sederhana dan mudah diterapkan untuk dua kelompok.
• Cocok untuk eksperimen yang membandingkan dua kelompok dengan distribusi normal.
❌ Kelemahan:
• Memerlukan asumsi tentang normalitas data dan kesetaraan varians antar kelompok (homoskedastisitas).
• Rentan terhadap outliers yang bisa mempengaruhi hasil.
Referensi:
• Field, A. (2013). Discovering Statistics Using IBM SPSS Statistics (4th ed.). SAGE Publications.
• Weiss, N. A. (2005). Introductory Statistics (8th ed.). Pearson Prentice Hall.
Formula:
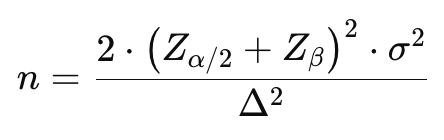 Di mana:
Di mana:
- σ2 = varians populasi.
- Δ = perbedaan yang diinginkan antara dua rata-rata.
- Zα/2 = skor Z sesuai tingkat signifikansi (misalnya 1.96 untuk 95%).
- Zβ = skor Z sesuai kekuatan uji yang diinginkan (misalnya 0.84 untuk 80%).
🎛️ Perhitungan Sampel untuk Uji Paired T-Test
🔍 Penjelasan Lengkap
Kapan Digunakan: Digunakan untuk menghitung jumlah sampel yang diperlukan dalam uji statistik paired t-test, yang membandingkan dua set data yang saling berhubungan. Uji ini digunakan ketika data yang diambil berasal dari dua pengukuran yang dilakukan pada unit yang sama (misalnya, pengukuran sebelum dan sesudah perlakuan pada subjek yang sama).
Contoh Penerapan (Studi Kasus): Sebuah studi ingin mengetahui apakah ada perubahan signifikan dalam berat badan pasien setelah mengikuti program diet selama 6 bulan. Data yang tersedia adalah pengukuran berat badan sebelum dan setelah program diet untuk setiap pasien. Berdasarkan data yang ada, peneliti perlu menghitung jumlah sampel yang dibutuhkan untuk mendeteksi perubahan rata-rata berat badan yang signifikan.
Kelebihan dan Kelemahan:
✅ Kelebihan:
• Cocok untuk eksperimen dengan pengukuran berulang pada subjek yang sama.
• Mengurangi variabilitas dengan membandingkan dua kondisi pada individu yang sama.
❌ Kelemahan:
• Hanya dapat digunakan jika data berpasangan, sehingga tidak cocok untuk kelompok yang independen.
• Perlu asumsi bahwa perbedaan antara dua pengukuran berdistribusi normal.
Referensi:
• Altman, D. G. (1991). Practical Statistics for Medical Research. CRC Press.
• Bland, M. (2015). An Introduction to Medical Statistics (4th ed.). Oxford University Press.
Formula:
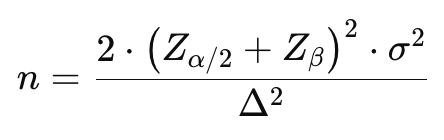 Di mana:
Di mana:
- σ2 = varians perbedaan antara pasangan.
- Δ = perbedaan yang diinginkan dalam rata-rata.
- Zα/2 = skor Z sesuai tingkat signifikansi (misalnya 1.96 untuk 95%).
- Zβ = skor Z sesuai kekuatan uji yang diinginkan (misalnya 0.84 untuk 80%).
🎛️ Perhitungan Sampel untuk Uji Chi-Square (Goodness of Fit atau Homogeneity)
🔍 Penjelasan Lengkap
Kapan Digunakan:
Uji Chi-Square digunakan untuk menentukan apakah ada perbedaan yang signifikan antara distribusi frekuensi yang diamati (observed) dan yang diharapkan (expected) dalam kategori tertentu. Uji ini dapat digunakan dalam dua bentuk:
• Goodness of Fit: Digunakan untuk menguji apakah data yang diamati sesuai dengan distribusi teoretis yang diharapkan.
• Homogeneity: Digunakan untuk menguji apakah dua atau lebih sampel independen berasal dari populasi yang memiliki distribusi yang sama.
Contoh Penerapan (Studi Kasus): Misalkan seorang peneliti ingin mengetahui apakah ada hubungan antara jenis kelamin dan preferensi warna di kalangan siswa. Mereka mengumpulkan data frekuensi preferensi warna dari sampel siswa laki-laki dan perempuan. Uji Chi-Square akan digunakan untuk membandingkan distribusi warna yang diamati dengan distribusi yang diharapkan berdasarkan hipotesis nol bahwa tidak ada perbedaan preferensi warna antara siswa laki-laki dan perempuan.
Langkah-Langkah Penghitungan:
1. Tentukan hipotesis nol (H₀) dan hipotesis alternatif (H₁).
2. Hitung frekuensi yang diharapkan (E) untuk setiap kategori.
3. Hitung nilai chi-square (χ²) dengan rumus:
χ² = Σ [(O - E)² / E], di mana O adalah frekuensi yang diamati dan E adalah frekuensi yang diharapkan.
4. Tentukan derajat kebebasan (df), yaitu (k - 1) untuk Goodness of Fit dan (r - 1)(c - 1) untuk Homogeneity.
5. Bandingkan nilai χ² yang dihitung dengan nilai χ² tabel untuk menentukan apakah hipotesis nol dapat ditolak.
Kelebihan dan Kelemahan:
✅ Kelebihan:
• Tidak memerlukan asumsi distribusi normal.
• Dapat digunakan untuk data kategorikal.
❌ Kelemahan:
• Memerlukan ukuran sampel yang cukup besar agar hasil uji dapat dipercaya.
• Tidak cocok untuk kategori dengan frekuensi yang sangat rendah (<5).
Referensi:
• Agresti, A. (2007). An Introduction to Categorical Data Analysis. Wiley-Interscience.
• Everett, B. (2015). Practical Statistics for Data Scientists. O'Reilly Media.
Formula:
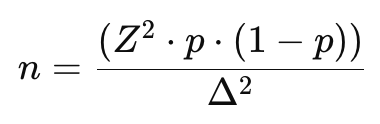 Di mana:
Di mana:
- p = proporsi yang diharapkan dalam kategori.
- Δ = margin kesalahan yang diinginkan.
- Z = skor Z untuk tingkat kepercayaan (misalnya, 1.96 untuk 95% confidence level).
🎛️ Perhitungan Sampel untuk Varians (Single Variance)
🔍 Penjelasan Lengkap
Kapan Digunakan: Digunakan untuk menentukan ukuran sampel yang diperlukan saat kita ingin memperkirakan varians populasi dengan tingkat kepercayaan tertentu. Ini sering digunakan dalam uji statistik yang berkaitan dengan sebaran atau variabilitas data dalam sebuah populasi tunggal.
Contoh Penerapan (Studi Kasus): Sebuah perusahaan ingin memperkirakan varians waktu yang dibutuhkan pelanggan untuk melakukan pembelian. Mereka menginginkan margin kesalahan tidak lebih dari 5 detik, dengan tingkat kepercayaan 95%. Perusahaan tersebut harus menghitung ukuran sampel yang diperlukan berdasarkan varians yang telah diketahui dari data sampel awal.
Kelebihan dan Kelemahan:
✅ Kelebihan:
• Memungkinkan penentuan ukuran sampel yang diperlukan untuk memperkirakan varians dengan presisi yang tinggi.
• Berguna dalam penelitian yang melibatkan data numerik yang sangat bervariasi.
❌ Kelemahan:
• Memerlukan estimasi awal dari varians populasi yang dapat mempengaruhi akurasi hasil.
• Asumsi normalitas sangat penting untuk perhitungan yang tepat.
Referensi:
• Cochran, W. G. (1977). Sampling Techniques (3rd ed.). John Wiley & Sons.
• Kish, L. (1965). Sociological Methodology. John Wiley & Sons.
Formula:
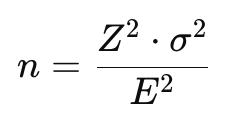 Di mana:
Di mana:
- Z = Skor Z yang digunakan berdasarkan tingkat kepercayaan (misalnya 1.96 untuk 95% confidence level).
- E = Margin kesalahan atau batas ketepatan yang diinginkan.
- σ2 = Varians populasi atau sampel.
🎛️ Perhitungan Sampel untuk Penelitian Eksperimental (Randomized Controlled Trial / RCT)
Formula 1. Jika berbasis perbandingan dua proporsi:
🔍 Penjelasan Lengkap
Kapan Digunakan: Digunakan ketika peneliti ingin membandingkan dua proporsi kejadian antara dua kelompok dalam penelitian eksperimen, seperti RCT (Randomized Controlled Trial). Ini sering digunakan untuk mengukur efektivitas pengobatan atau intervensi dengan membandingkan dua grup, misalnya grup yang diberi perlakuan dan grup kontrol.
Contoh Penerapan (Studi Kasus): Sebuah penelitian ingin mengetahui apakah obat A lebih efektif daripada obat B dalam mengurangi kejadian penyakit X. Dari uji coba sebelumnya, proporsi kejadian penyakit X pada grup obat A adalah 30% (P1 = 0.30), dan pada grup obat B adalah 50% (P2 = 0.50). Diketahui tingkat signifikansi 5% (Zα/2 = 1.96) dan kekuatan uji 80% (Zβ = 0.84).
Kelebihan dan Kelemahan:
✅ Kelebihan:
• Memungkinkan penilaian yang kuat terhadap perbedaan antara dua grup dalam penelitian eksperimental.
• Cocok untuk eksperimen dengan dua intervensi atau dua kelompok yang berbeda.
❌ Kelemahan:
• Membutuhkan asumsi proporsi yang dapat dihitung dengan baik di populasi.
• Tidak cocok jika data tidak dapat dipasangkan atau kelompok tidak independen.
Referensi:
• Freedman, L. S., Pisani, R., & Purves, R. (2007). Statistics: The Art and Science of Learning from Data. Pearson.
• Piantadosi, S. (2017). Clinical Trials: A Methodologic Perspective (2nd ed.). Wiley-Interscience.
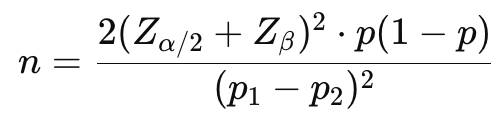 Di mana:
Di mana:
- p1,p2 = proporsi keberhasilan pada masing-masing kelompok.
- p = (p1+p2)/2.
- Zα/2 = skor Z sesuai tingkat signifikansi (misalnya 1.96 untuk 95%).
- Zβ = skor Z sesuai kekuatan uji yang diinginkan (misalnya 0.84 untuk 80%). Hitung Sampel
- σ2 = varians dari pengukuran (asumsi sama untuk kedua kelompok).
- Δ = perbedaan rata-rata yang dianggap signifikan secara klinis.
- Zα/2 = skor Z sesuai tingkat signifikansi (misalnya 1.96 untuk 95%).
- Zβ = skor Z sesuai kekuatan uji yang diinginkan (misalnya 0.84 untuk 80%).
Formula 2. Jika berbasis perbandingan dua rata-rata:
🔍 Penjelasan Lengkap
Kapan Digunakan: Rumus ini digunakan dalam penelitian eksperimental, khususnya untuk desain penelitian dengan dua kelompok yang diberikan perlakuan berbeda. Dalam konteks Randomized Controlled Trial (RCT), rumus ini digunakan untuk menentukan jumlah sampel yang dibutuhkan untuk membandingkan dua rata-rata kelompok yang diacak.
Contoh Penerapan (Studi Kasus): Sebuah RCT dilakukan untuk menguji efektivitas dua jenis obat terhadap penurunan tekanan darah. Kelompok 1 diberikan obat A dan kelompok 2 diberikan obat B. Peneliti ingin mengetahui perbedaan rata-rata tekanan darah antara kedua kelompok dengan tingkat signifikansi 5% dan kekuatan uji 80%. Varians pada masing-masing kelompok diketahui, dan perbedaan rata-rata yang dianggap signifikan adalah 10 mmHg.
Kelebihan dan Kelemahan:
✅ Kelebihan:
• Menyediakan pembanding yang jelas antara dua kelompok perlakuan yang berbeda dalam uji klinis.
• Sesuai untuk desain penelitian terkontrol dengan acakan.
❌ Kelemahan:
• Memerlukan varians populasi yang dapat diperkirakan atau diestimasi dari sampel.
• Asumsi bahwa varians di kedua kelompok adalah homogen (sama) terkadang sulit dipenuhi.
Referensi:
• Piantadosi, S. (2005). Clinical Trials: A Methodologic Perspective (2nd ed.). Wiley-Interscience.
• Machin, D., Campbell, M. J., & Tan, S. B. (2011). Sample Sizes for Clinical, Epidemiological, and Social Research (2nd ed.). Wiley.
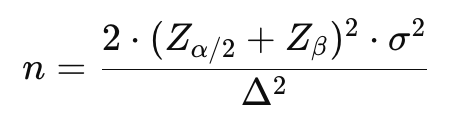 Di mana:
Di mana:
🎛️ Perhitungan Sampel Krejcie-Morgan
🔍 Penjelasan Lengkap
Kapan Digunakan: Rumus Krejcie-Morgan digunakan untuk menentukan ukuran sampel yang dibutuhkan berdasarkan jumlah populasi yang diketahui secara pasti. Cocok untuk penelitian survei atau kuantitatif dengan populasi terbatas, dan mempertimbangkan tingkat kepercayaan serta margin of error.
Contoh Penerapan (Studi Kasus): Jika seorang peneliti ingin meneliti persepsi guru di sebuah kota dengan populasi 500 orang, dan menginginkan tingkat kepercayaan 95% serta margin of error 5%, maka rumus Krejcie-Morgan dapat digunakan untuk menentukan jumlah responden yang representatif.
Kelebihan dan Kelemahan:
✅ Kelebihan:
• Tidak memerlukan nilai standar deviasi populasi.
• Praktis dan cepat digunakan, terutama jika dibantu tabel Krejcie-Morgan.
❌ Kelemahan:
• Tidak fleksibel untuk margin of error dan tingkat kepercayaan yang berbeda dari standar.
• Kurang akurat untuk populasi yang sangat besar atau sangat kecil (karena asumsi umum proporsi).
Referensi:
• Krejcie, R. V., & Morgan, D. W. (1970). Determining Sample Size for Research Activities. Educational and Psychological Measurement, 30(3), 607–610.
• Israel, G. D. (1992). Determining Sample Size. University of Florida IFAS Extension.
Formula:
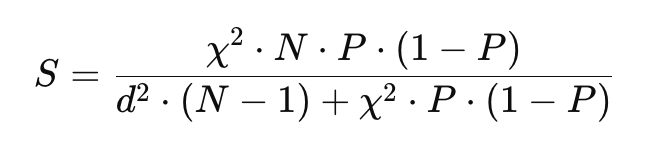 Di mana:
Di mana:
- S = ukuran sampel.
- X² = nilai chi-square pada df = 1 dan tingkat signifikansi 0.05 (biasanya 3.841).
- N = jumlah populasi.
- P = proporsi populasi (umumnya diasumsikan 0.5).
- d = margin of error yang dapat diterima (umumnya 0.05).